2.1.1 DEFINICION DE LAS FUNCIONES TRIGONOMETRICAS.

Considérese el triangulo rectángulo BAC.

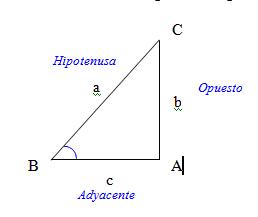
Cateto o lado adyacente. Es el lado adyacente al ángulo pero que no es la hipotenusa.

Cateto o lado opuesto. Es el lado opuesto al ángulo pero que no es la hipotenusa.

Hipotenusa. Es el lado opuesto al ángulo de 90º en el triangulo rectángulo.

Si se designan los lados con minúsculas que corresponden a las mayúsculas de los vértices opuestos, las funciones trigonometricas del ángulo B se pueden expresar como sigue:

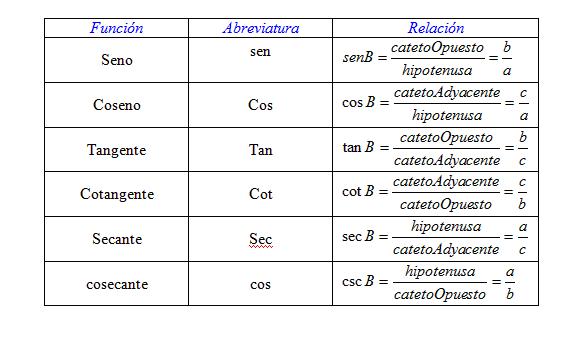
El uso de MNEMONICOS ayuda a recordar las relaciones trigonometricas.

SOHCAHTOA

Se puede interpretar como:

SOH -  Seno Opuesto Hipotenusa

CAH - Coseno Adyacente Hipotenusa

TOA - Tangente Opuesto Hipotenusa

2.1.2 COFUNCIONES

Ángulos complementarios: cofunciones.

Dos ángulos agudos se llaman complementarios si su suma es un ángulo recto. Puesto que la suma de los ángulos de cualquier triangulo es 180º, se infiere que en un triangulo rectangulo, los dos ángulos agudos son complementarios.

De la cual obtenemos

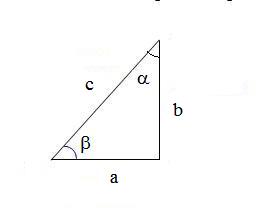
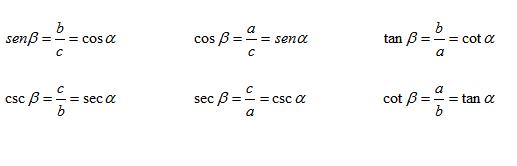
Debido a estas relaciones las funciones seno y coseno, tangente y cotangente, y secante y cosecante se llaman cofunciones una de la otra. Las identidades mostradas arriba pueden expresarse en palabras como sigue:

Las cofunciones de ángulos complementarios son iguales.

El seno de un ángulo es igual al coseno de su complemento

La tangente de un ángulo es igual a la cotangente de su complemento.
La secante de un ángulo es igual a la cosecante de su complemento.

A continuación se dan algunos ejemplos:

Sen 30º = cos 60º                 tan 40º = cot 50º           sec 80º = csc 10º

Tabla 2.1

Ejemplos

      a) sen 62 º = cos (90º-62º) = cos 28º

   b) cos  π/4 = sen (π/2 - π/4) = π/4

TEOREMA DE PITAGORAS

El Teorema de Pitágoras dice:

En un triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la Hipotenusa.

Formalmente, si un triángulo tiene catetos de tamaño a y b, el valor c de la Hipotenusa está determinado por:

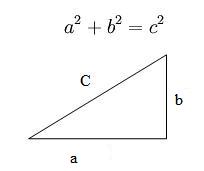
Ejemplos.

1º Sabiendo que la hipotenusa y un cateto de un triangulo rectángulo valen, respectivamente, 13 y 5 hallar el valor de las funciones trigonometricas de los ángulos agudos.

Por el teorema de Pitágoras se tiene:

b=√c²-a² = √13²-5²=√144=12

Luego, los valores de las funciones trigonometricas son:

Sen B = cos C = 5/13  = 0.3846                    cot B = tan C = 12/5 = 2.40

Cos B = sen C = 12/13 = 0.9230                   sec B = csc C = 13/12 = 1.083

Tan B = cot C = 5/12 = 0.4166                     csc B = sec C = 13/5 = 2.60

2º Dada sec B = 3/2, calcular las demas funciones trigonometricas de este angulo.

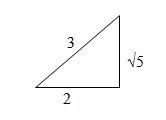
                               B= √3²-2²=√5

                               sen B = √5/3=0.745               cos B = 2/3 = 0.666

                               tan B = √5/2=1.118                cot B = 2/√5 = 0.894

                               sec B = 3/2 = 1.50                  csc B = 3/√5 = 1.341

Angulos de 30º y de 60º.

Sea ABC un triangulo equilátero. La perpendicular DA biseca el lado BC y el ángulo BAC. Por tanto, si el lado BC es igual a 2, el lado BD del triangulo rectángulo BDA vale 1, y la altura AD mide

√4-1 = √3

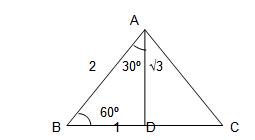
Se tiene entonces, según las definiciones fundamentales y las relaciones que ligan las funciones de dos ángulos complementarios:

Sen 30º = cos 60 º = ½ = 0.5

Cos 30º = sen 60º = √3 /2 = 0.8660

Tan 30º = cot 60º = 1/√3 = √3/3 = 0.5774

Cot 30º = tan 60º = √3 = 1.732

Sec 30º = csc 60º = 2/√3 = 1.155

Csc 30º = sec 60º = 2

Angulo de 45º

Para calcular las funciones del ángulo de 45º, basta considerar un triangulo rectángulo isósceles, cuyos catetos midan √2.

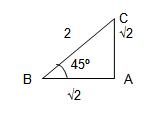
La longitud de la hipotenusa es 2, y las funciones trigonometricas tienen los siguientes valores:

Sen 45º = cos 45º = √2/2 = 0.7071

Tan 45º = cot 45º = 1

Sec 45º =csc 45º = √2 = 1.4142