|
El ángulo considerado como
amplitud de rotación. Considérese dos rectas superpuestas en un principio, y que una de ellas, OA permanece fija mientras
la otra, OB, gira alrededor de un punto fijo O de la primera, quedando siempre en el mismo plano: la abertura comprendida
entre la posición inicial y la posición final de OB, se llama ángulo
OAB.
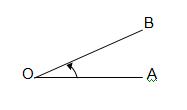
A la recta que se ha movido
para engendrar el ángulo se le llama lado móvil, y a su movimiento, rotación.
Angulo es la abertura comprendida entre
la posición inicial y la posición final de una recta que ha girado alrededor de uno de sus puntos, permaneciendo siempre en
el mismo plano.
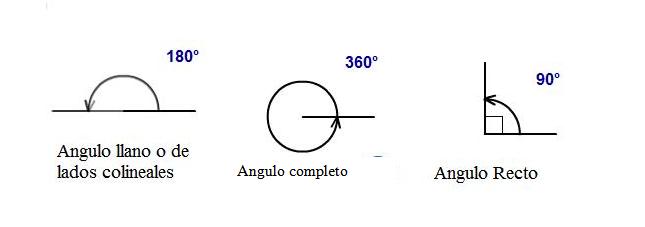
Ángulos de una vuelta, de lados colineales y recto.
Si el lado móvil se mueve
da manera que la posición final llegue a coincidir con la posición inicial, el ángulo generado se llama ángulo perigonal o completo (ángulo de una vuelta).
Cuando el lado móvil llegue a formar una misma
recta con la posición inicial, el ángulo que resulta se llama ángulo
llano (ángulo de lados colineales), y si es perpendicular a la posición inicial, el ángulo formado se llama ángulo recto.
Las unidades utilizadas para
la medida de los ángulos del plano son:
Grado centesimal Las unidades se expresan en grado
centesimal o gradián. unidad angular que divide la circunferencia en 400 grados centesimales.
Grado sexagesimal las unidades se expresan en grados. unidad angular que divide una circunferencia en 360º.
Radián (cíclico) las unidades se expresan
en unidades cíclicas
unidad angular natural en
trigonometría, será la que aquí utilicemos, en una circunferencia completa hay 2π radianes.
El símbolo del grado:
°
Se usa un circulo pequeño ° enseguida
de un numero para denotar los grados.
Por ejemplo 90° significa
90 grados.
Un círculo completo tiene 360°
La mitad de un círculo tiene 180°
Un cuarto de círculo tiene 90°

1.2 SISTEMA SEXAGESIMAL
1.2.1 Descripcion
El sistema sexagesimal es un sistema de numeración posicional que emplea la base sesenta. Tuvo su origen en la antigua Babilonia.
El uso del número sesenta como base para
la medición de ángulos, coordenadas y medidas de tiempo se vincula a la vieja astronomía y a la trigonometría. Era común medir
el ángulo de elevación de un astro y la trigonometría utiliza triángulos rectángulos.
El grado sexagesimal es la nonagésima
(1/90) parte de un ángulo recto.
El grado sexagesimal, como unidad
del sistema de medida de ángulos sexagesimal, esta definido partiendo de que un ángulo recto tiene 90º (90 grados sexagesimales),
y sus divisores el minuto sexagesimal, y el segundo sexagesimal, están definidos del siguiente modo:
1 ángulo recto = 90° (grados sexagesimales).
1 grado sexagesimal = 60′ (minutos
sexagesimales).
1 minuto sexagesimal = 60″ (segundos
sexagesimales).
Notación decimal
Una cantidad en grados se puede
expresar en forma decimal, separando la parte entera de la decimal con la coma decimal, en la forma normal de expresar cantidades
decimales, por ejemplo.
23,2345° 12,32°
-50,265° 123,696°
Notación sexagesimal
Podemos expresar una cantidad en
grados minutos y segundos, las partes de grado inferiores al segundo se expresan como parte decimal de segundo, ejemplo:
12°34′34,2″ 13°3′23,8″
124°45′34,70″ -2°34′10″
Teniendo cuidado como norma de notación,
no dejar espacio entre las cifras, es decir:
escribir 12°34′34,2″
y no 12° 34′ 34,2″
Podemos también representar en forma
decimal la medida de un ángulo en representación sexagesimal teniendo en cuenta que:
1’ = (1/60)° = 0.01666667°
1” = (1/60)′ =
(1/3600)° = 0.00027778°
Así 12°15′23″ = 12°
+ 15(1/60)° + 23(1/3600)° ≈ 12,25639°
EJEMPLOS.
Expresar en forma decimal los ángulos siguientes
- 38°25´ = 38+25(1/60)
° = 38.41667
- 59°53´ = 59+53(1/60)
° = 59.8833
- 24°37´52” = 24+37(1/60)+52(1/3600) = 24.6311

1.3 SISTEMA CICLICO
1.3.1 DESCRIPCION
En el sistema cíclico la unidad de medida
es el radian. El radián se define como el ángulo que limita un arco de circunferencia cuya longitud es igual al radio de la circunferencia.


1.4 SISTEMA CENTESIMAL
1.4.1 DESCRIPCION
En este sistema, el ángulo recto esta dividido
en 100 partes iguales, llamadas grados centesimales. Cada grado constituye la unidad centesimal y se divide en 100 minutos, cada minuto en 100 segundos.
Notación. Se escribe la letra G a manera
de exponente del numero que los expresa, y las comillas para minutos y segundos se escriben dirigidas hacia la derecha.
Ejemplo.
47 grados. 34 minutos, 25 segundos se escriben:
47G34`25``
En este sistema los minutos se expresan
como decimales de grado y los segundos como decimales de minuto.
Ejemplo.
48G25`37``, se puede escribir
48G25.37`, o mejor
48.2537G

|



